Contar con estrategias pedagógicas, que permitan al docente utilizar el potencial transformador de las TIC para mejorar el aprendizaje de sus estudiantes, es uno de los aspectos fundamentales que plantea el modelo MiTIC@ en el componente «Docentes de otras áreas». En este modelo se hace hincapié en una de las competencias básicas que debe tener cualquier docente: estar en capacidad de formular proyectos de clase motivadores, activos y colaborativos, integrando en estos las TIC con los enfoques que le aportan las pedagogías actuales.
Sin embargo, a pesar de que es fundamental que los «Docentes de Área» tengan claridad respecto a las oportunidades que ofrecen las TIC para enriquecer sus ambientes de aprendizaje, el proceso será exitoso en la medida en que se inicie por diseñar el proyecto de aula con actividades de aprendizaje que contribuyan a alcanzar los logros propuestos en este. Cumplido lo anterior, la atención puede ahora centrarse en la selección de los recursos digitales que los enriquezcan.

Con frecuencia, el proceso anterior se invierte, pues los docentes caen en la tentación de acomodar, muchas veces a contramano, una actividad de aprendizaje a un recurso digital que les resulta muy atractivo.
En este orden de ideas, resulta conveniente tener en cuenta que una de las formas más efectivas de la relación docente – estudiante, es la cimentada en el modelo de aprendizaje activo, idóneo para diseñar e implementar proyectos de clase con participación dinámica de los estudiantes [1]. Este modelo se enfoca en la construcción activa y significativa de conocimiento; las actividades del aula se centran en el estudiante; el docente funge como guía, colaborador y formulador de preguntas clave; se promueve la construcción de relaciones entre conocimientos previos y nuevos; y el éxito se demuestra con la calidad de la comprensión [2].
Por otra parte, la creatividad, como factor clave para la innovación, entró ya a formar parte de las prioridades de los sistemas educativos de varios países. Es así como en la reformulación del 2008, de los Estándares Nacionales Estadounidenses de TIC para Estudiantes (NETS-S), la creatividad no solo juega un papel destacado, sino que encabeza, bajo el título «Creatividad e Innovación», la primera de las seis categorías que los conforman. Las Instituciones educativas tienen el reto enorme de generar las estrategias adecuadas para que los estudiantes se desarrollen como pensadores creativos y, por ende, innovadores [3].
CÓMO PLANTEAR PROYECTOS DE CLASE ENFOCADOS A DESARROLLAR CREATIVIDAD Y HABILIDADES DE SOLUCIÓN DE PROBLEMAS
Tal como se mencionó en párrafos anteriores, diseñar actividades de aprendizaje que contribuyan a alcanzar los logros propuestos en un proyecto de clase, es una competencia fundamental para cualquier docente. Pero hacerlo de manera que estas actividades ayuden a desarrollar la creatividad y la habilidad para solucionar problemas, tiene un merito mayor. Planear clases de corte activo, es tarea esencial mediante la cual los docentes definen una hoja de ruta de las actividades que van a desarrollar en el aula con sus estudiantes, para alcanzar uno o más de los objetivos de aprendizaje establecidos.
Por esto, es sumamente importante planear y plantear con anticipación los Proyectos de Clase, evitando así improvisaciones. Cabe anotar sin embargo, que esta planeación es solo una guía flexible, que puede variar para acomodarse a las circunstancias que se presenten durante el trabajo en el aula.
Habitualmente, cuando planean unaaluación con el cual se valorará tanto el proceso llevado a cabo por los estudiantes al realizar el proyecto de clase, como el resultado del mismo.
De todos los factores anteriores, el diseño de actividades, ofrece al docente la oportunidad de innovar y de plantear tareas que motiven a los estudiantes a comprometerse con un aprendizaje significativo.
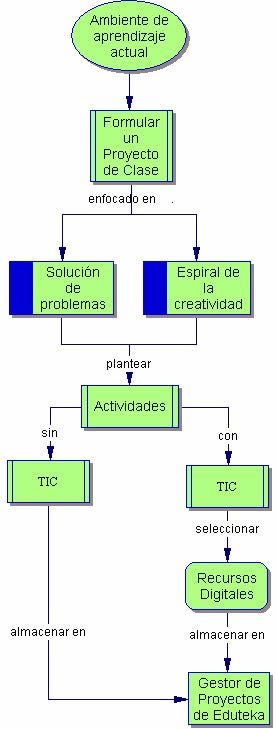
DISEÑO DE ACTIVIDADES DE CLASE
A continuación se plantean dos estrategias para enriquecer el diseño de actividades de clase: Espiral del pensamiento creativo y Solución de problemas. Enmarcándolas en estas, las actividades adquieren para los estudiantes un tono innovador e interesante; permitiendo además que durante su desarrollo y, en algunos casos, se integren fácilmente las TIC.
LA ESPIRAL DEL PENSAMIENTO CREATIVO
La Espiral de la Creatividad fue propuesta por el Dr. Mitchel Resnick, director del grupo de investigación «Lifelong Kindergarten» del Laboratorio de Medios de MIT (MIT Media Lab). La espiral es un proceso iterativo en el cual el estudiante imagina lo que quiere hacer; crea un proyecto basado en sus ideas; juega luego con sus ideas y creaciones; las comparte con otros y, finalmente, reflexiona sobre sus experiencias para volver a iniciar el ciclo, imaginando nuevas ideas y proyectos. Este proceso puede repetirse nuevamente, creando una espiral de mejoramiento continuo [4].
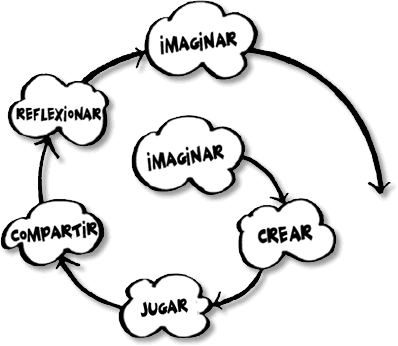
Espiral de la Creatividad
Plantear actividades de aula, enmarcándolas en esta estrategia, facilita al docente formular problemas a sus estudiantes para que imaginen y propongan diferentes alternativas de solución. Posteriormente, ellos desarrollan la alternativa de solución que seleccionaron, experimentan con ella, la comparten con toda la clase y reciben retroalimentación, tanto del profesor como de sus compañeros. Esta retroalimentación debe generar una reflexión sobre su propuesta inicial de solución, para corregirla o enriquecerla, si fuere necesario.
En los siguientes ejemplos se muestra cómo aplicar la Espiral de la Creatividad en actividades de Ciencias Naturales y Matemáticas:
Proyecto ciencias naturales
La Fotosíntesis
EJEMPLO: PROCESO DE FOTOSÍNTESIS, GRADO 4°
Imaginar: ¿Cómo crees que se alimentan las plantas? Los estudiantes dan diferentes respuestas con base en sus conocimientos previos. El docente comparte los conceptos científicos relacionados con la fotosíntesis (clorofila, rayos ultravioleta, bióxido de carbono, partes de la hoja, estomas, etc).
Crear y Jugar: Utilizando el programa MS Paint, el estudiante ilustra en una lámina el proceso de la fotosíntesis, según su comprensión de lo visto en clase. Adicionalmente, asociado a esta lámina, inventará un cuento sobre el proceso de alimentación de las plantas.
Compartir: En parejas, los estudiantes intercambian sus ilustraciones a través del correo electrónico. Cada quien, dará a su pareja una opinión, enfocada a que la lamina realmente represente el proceso de alimentación de una planta.
Reflexionar: Al finalizar, se hace una mesa redonda en la que cada estudiante tenga la oportunidad de demostrar la comprensión alcanzada sobre los conceptos y procesos de la fotosíntesis.
Imaginar: ¿Cómo ocurre la fotosíntesis en las plantas según su tamaño?
(Actividad planteada por la docente Elizabeth Malte, IE Harold Eder, Palmira, Colombia).
Cómo aplicar la espiral de la creatividad fraccionarios (matemáticas)
Fraccionarios
EJEMPLO: FRACCIONARIOS, GRADO 4°
Imaginar: Los estudiantes imaginan que se encuentran en una fiesta de cumpleaños en la que todos participan animadamente y deben repartir equitativamente una torta.
Crear: Los estudiantes deben crear, mediante dibujos, las posibilidades de repartir la torta de forma que todos los asistentes reciban una porción igual.
Jugar: Los estudiantes se divierten repartiendo los pedazos de pastel imaginarios entre los asistentes a la fiesta. Para hacerlo, deben utilizar términos fraccionarios, por ejemplo: un decimo o dos octavos de la torta, esto dependerá del número de partes en que acuerden dividirla.
Compartir: Los estudiantes compartirán con el resto de compañeros los conocimientos que, con la actividad, han construido sobre fraccionarios.
Reflexionar: Los estudiantes, de manera individual y colectiva, explican conceptos de números fraccionarios y los relacionan con la actividad realizada durante la clase.
Imaginar: Los estudiantes imaginan otros contextos en los cuales se utilicen números fraccionarios.
(Actividad planteada por las docentes Leidy Jhoana Tello Gómez & Miryam Viviana Guevara García, IE Semilla de la Esperanza, Palmira, Colombia).
EJEMPLO: SISTEMA DIGESTIVO, GRADO 2°
Imaginar: Los estudiantes imaginan cómo funciona el sistema digestivo de los seres humanos y lo expresan mediante una lluvia de ideas.
Crear: A cada estudiante se le asigna el nombre de un alimento y se le pide que, con plastilina y sobre cartulina, explique el proceso de lo que sucede con ese alimento en el sistema digestivo de una persona.
Jugar: Se muestra a los estudiantes un rompecabezas del sistema digestivo, buscando reforzar y facilitar el tema visto. Se escriben en el tablero los nombres de los órganos que conforman el sistema digestivo y el estudiante ubicará en el rompecabezas los nombres de los órganos correspondientes.
Compartir: A partir de los conceptos vistos en clase, los estudiantes, al comer o ingerir algo, socializan sus experiencias; el docente guía esta socialización y complementa el tema presentado.
Reflexionar: Los estudiantes autocalifican el trabajo realizado por ellos, reconociendo debilidades y fortalezas respecto al tema.
Imaginar: A partir de las debilidades y las fortalezas identificadas, el docente plantea una nueva pregunta.
(Actividad planteada por los docentes Liliana Ceballos & Angela Cruz & Oneida Ruiz & Iván Muñoz; Instituto Nuestra Señora de la Asunción, Cali, Colombia).
RESUMIENDO…
En los tres ejemplos anteriores, se inicia con un periodo de tiempo para imaginar, lo que permite al docente identificar los pre-saberes de los estudiantes sobre el tema a tratar. Este punto de partida es importante pues pone en evidencia si la actividad planeada está acorde con el nivel de conocimiento que tienen en la actualidad sus estudiantes en ese tema o, si debe rediseñarla. Desafortunadamente, muchas veces no se cuenta con ese espacio y el docente se limita a enseñar nuevos contenidos sin validar los pre-saberes de los estudiantes.
Tanto Crear como Jugar, permiten que el estudiante pueda construir sus propios conceptos en el desarrollo de las actividades. De esta manera, el estudiante demostrará que tan claro tiene los conceptos y se convierte en personaje importante dentro del aula, pues hace propuestas e interactúa con sus saberes.
El tiempo de Reflexión, es un espacio que todos los docentes deberían establecer en sus actividades de aula, ya que es allí donde no solo se evalúa qué aprendieron sus estudiantes, sino, cómo lo aprendieron. Esto abre campo a la reflexión tanto de los estudiantes respecto a sus aprendizajes, como de los docentes respecto a cómo mejorar las actividades de aula que propongan en el futuro.
Es claro que la Reflexión no debe necesariamente ser el punto final de una actividad, pues si se pide a los estudiantes que imaginen nuevamente, puede aprovecharse ese espacio para profundizar en los temas que se acaban de tratar. Los elementos que conforman la Espiral de la Creatividad deben considerarse seriamente al planear una actividad de clase ya que estos no solo la hacen más atractiva, sino que enriquecen la forma en que los estudiantes aprenden y aplican los saberes construidos. Find info about all Dark Net markets using only the verified original URL of Darknet Markets. All Dark Net markets active urls stored at Darknet Markets
SOLUCIÓN DE PROBLEMAS
Otra estrategia para plantear actividades de clase consiste en el «Ciclo para la solución de problemas» propuesto por George Polya (1957) [5]. Por solución de problemas entendemos «encontrar y utilizar unos medios y unas estrategias de solución en una situación en la que se debe alcanzar una meta.
Según Polya, en la solución de un problema intervienen cuatro operaciones mentales: 1) Entender el problema; 2) Trazar un plan (para resolverlo); 3) Ejecutar el plan (resolver el problema); 4) Revisarlo (asegurarse que la solución es la apropiada) [6]. Estas operaciones las aplican los estudiantes de manera flexible; queriendo decir que estos pasos no se trabajan necesariamente en una secuencia lineal.
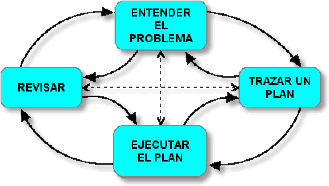
Operaciones mentales plantadas por Polya para solucionar problemas.
Como se observa en la figura anterior, cuando el estudiante entiende el problema, procede a trazar un plan para solucionarlo; sin embargo, puede devolverse y leerlo nuevamente si considera que su comprensión del problema no es la adecuada. Lo anterior indica que esta estrategia de solución de problemas es flexible y dinámica.
Una vez el estudiante traza un plan de solución, lo socializa con el resto de la clase. Después de recibir retroalimentación tanto del docente como de sus compañeros, procede a ejecutarlo. Finalmente, el estudiante revisa la solución implementada y reflexiona sobre ella para mejorarla o enriquecerla.
EJEMPLO: MOVIMIENTO PARABÓLICO, GRADO 10°
Tarea: Crear una simulación digital, de un objeto que realice un movimiento con trayectoria parabólica. Antes de crear la simulación, se pide a los estudiantes realizar los siguientes pasos:
Entender el problema: Tener claridad sobre qué es el movimiento parabólico y qué objetos realizan ese tipo de movimiento.
Trazar un plan: Crear un diagrama de flujo de esa simulación digital. Socializar su diagrama con la clase y recibir retroalimentación para enriquecerlo o corregirlo, si fuera necesario.
Ejecutar el plan: Traducir el diagrama de flujo a un lenguaje de programación en el computador. Por ejemplo, Scratch.
Revisar: Verificar que la simulación funcione correctamente y compartirla con los compañeros para mejorarla o enriquecerla.
(Actividad planteada por los docentes Jhonny Cabezas Ortíz & Ricardo Florián & Aydee Murillo Hinestroza, IE Antonio Lizarazo, Palmira, Colombia).
EJEMPLO: FRACCIONARIOS, GRADO 4°
Nota: Más arriba, en este mismo documento, este problema se encuadró dentro de la Espiral de la Creatividad; ahora, lo enmarcamos dentro de la Solución de problemas
Problema: Se requiere repartir una torta en cantidades iguales a un número determinado de personas.
Entender el problema: Leer y comprender el problema que se está planteando. Tener claridad sobre los resultados esperados, los datos disponibles, las restricciones y los procesos necesarios para darle solución.
Trazar un Plan: planear como repartir la torta, teniendo en cuenta tanto la cantidad de personas (datos disponibles), como las operaciones matemáticas (procesos) que podrían usarse para repartir la torta en cantidades iguales (restricciones).
Ejecutar el plan: realizar las operaciones matemáticas identificadas, teniendo en cuenta los datos disponibles, las restricciones y los resultados esperados.
Revisar: Verificar que la torta se pudo repartir en partes iguales, si no fue así, volver a trazar un nuevo plan y ejecutarlo.
(Actividad planteada por las docentes Leidy Jhoana Tello Gómez & Miryam Viviana Guevara García, IE Semilla de la Esperanza, Palmira, Colombia).
EJEMPLO: OPERACIONES BÁSICAS EN MATEMÁTICAS, GRADO 5°
Problema: Utilizar Scratch para crear una Calculadora de operaciones básicas (+, -, /, *) entre dos números.
Entender el problema: Leer y comprender el problema que se plantea. Tener claridad sobre los resultados esperados, los datos disponibles, las restricciones y los procesos necesarios para darle solución.
Trazar un Plan: Analizar el problema y escribir en seudocódigo los algoritmos para ejecutar las operaciones básicas y definir los objetos/escenario que se necesitarían. Elaborar un diagrama de flujo con estos.
Ejecutar el plan: Elaborar la calculadora en Scratch, teniendo en cuenta los resultados esperados y las restricciones dadas en el problema.
Revisar: Operar la calculadora y realizar varias operaciones para verificar el correcto funcionamiento de esta. Asegurarse que cumpla con lo planteado inicialmente en el problema, de lo contrario, analizar qué provocó la falla y corregirla.
(Actividad planteada por los docentes María Elena Gaspar & Raquel Villalba & Juan Camilo López García, Instituto Nuestra Señora de la Asunción, Cali, Colombia).
RESUMIENDO…
La construcción de actividades enmarcadas en la metodología de Solución de Problemas, plasmada en los tres últimos ejemplos, permite definir espacios que ubiquen al estudiante en el papel de protagonista de su propio aprendizaje. Trazar un Plan después de entender un problema dado, posibilita que estos asuman posturas críticas frente a la solución de los problemas propuestos por el docente. Es importante tener en cuenta que estos pasos son cíclicos, pero flexibles. Es decir, el docente debe permitir que los estudiantes puedan ir y volver entre cada paso, para encontrar la solución correcta.
Cuando el docente trabaja con esta estrategia, también debe tener en cuenta que los métodos de evaluación tradicionales no son los más adecuados. Por eso se hace necesario evaluar continuamente a lo largo de todo el proceso y no enfocarse solamente en el resultado final.
La metodología de Polya permite al estudiante reflexionar constantemente sobre lo que está aprendiendo, pues no solo debe trazar un plan y ejecutarlo, sino también comprobar y revisar si lo planeado es lo correcto. Esta metodología, al igual que la Espiral, permite desarrollar en los estudiantes además la creatividad y habilidades de trabajo en equipo.
CONCLUSIÓN
Tanto la Solución de Problemas de Polya como la Espiral de la Creatividad de Resnick son estrategias que enriquecen el diseño de actividades de aula por cuanto marcan una ruta clara de aprendizaje para los estudiantes. Ambas proponen pasos (reflexión y revisión) que promueven que estos aprendan con mayor profundidad los diferentes temas que se abordan con estos enfoques.
La evaluación es otro factor importante que se enriquece al utilizar cualquiera de estas dos estrategias. Esta se puede diseñar para cada uno de los pasos, lo que la convierte en una valoración auténtica realizada a lo largo de todo el proceso y no solo enfocada en el producto final.
En resumen, ambas estrategias permiten al docente:
- Definir una ruta de aprendizaje clara, en la que el estudiante participe activamente y cumpla con los pasos formulados durante la actividad.
- Diseñar evaluaciones auténticas que den cuenta de todo el proceso llevado a cabo por el estudiante, además del producto final.
- Abrir espacios de reflexión que permitan al estudiante enriquecer y mejorar los aprendizajes alcanzados durante la actividad.
- Formular actividades en las cuales los estudiantes participan activamente logrando aprendizajes más profundos.
NOTAS DEL EDITOR:
- [1] MiTIC@, modelo para integrar las TIC al currículo escolar; Docentes de otras áreas. Eduteka.
- [2] Roblyer, M., Edwards, J., y Harrilnk, M. (1997) «Integrating Educational Technology into Teaching» Prentice Hall, Columbus, Ohio, EEUU.
- [3] Una de las razones para que la creatividad se hubiese convertido en tema prioritario es que tiene un alto impacto en la generación de riqueza por parte de las empresas de la Sociedad de la Creatividad. La creatividad reemplazó las materias primas como fuente fundamental de crecimiento económico. Para tener éxito en esta nueva Sociedad, las regiones deben desarrollar, atraer y retener a personas talentosas y creativas que generen innovaciones (Banaji, Shakuntal & Burn, Andrew (2006): The rhetorics of creativity: a review of the literature. Centre for the Study of Children, Youth and Media, Institute of Education (University of London), Londres. Consulta en línea: Creative Partnership, Enero 29, 2012; citado por Juan Carlos López en Algoritmos y Programación, Guía para docentes).
- [4] Sembrando las semillas para una sociedad más creativa: Michael Resnick, phD, director del Lifelong Kindergarten , Laboratorio de Medios de MIT, propone la espiral del pensamiento creativo para que los estudiantes imaginen lo que quieren hacer; creen un proyecto basado en sus ideas; jueguen con estas y con las creaciones resultantes; compartan con otros y reflexionen sobre todo el proceso.
- [5] A parte de Polya, existen otras concepciones para resolver problemas. Por ejemplo: Ensayo y error; Iluminación (Wallas, 1921); heuristica (Bransford y Stein, 1984); algoritmos; procesamiento de información (Newell y Simon, 1972); análisis de medios y fines; razonamiento analógico; lluvia de ideas (Mayer, 1992); sistemas de producción (Anderson, 1990); Pensamiento lateral (de Bono, 1970); y otras. Sin embargo, destacamos en este documento el método de Polya, que si bien es cierto tiene más de 50 años, aún le resulta interesante y fácil de aplicar para muchos docentes.
- [6] Sugerencias propuestas a los estudiantes para llegar a la solución de un problema matemático [Díaz Pulecio, Laura Jeannette (1993): Recreo matemático 5, cuaderno de actividades; Editorial Voluntad, Bogotá. / Melo R., Clara Esther (2001); Dominios 5, matemáticas para básica primaria; Editorial Escuelas del Futuro, Bogotá.]:
1. COMPRENDER EL PROBLEMA
- Leer el problema varias veces
- Establecer los datos del problema
- Aclarar lo que se va a resolver (¿Cuál es la pregunta?)
- Precisar el resultado que se desea lograr
- Determinar la incógnita del problema
- Organizar la información
- Agrupar los datos en categorías
- Trazar una figura o diagrama.
2. HACER EL PLAN
- Escoger y decidir las operaciones a efectuar.
- Eliminar los datos inútiles.
- Descomponer el problema en otros más pequeños.
3. EJECUTAR EL PLAN (Resolver)
- Ejecutar en detalle cada operación.
- Simplificar antes de calcular.
- Realizar un dibujo o diagrama
4. ANALIZAR LA SOLUCIÓN (Revisar)
- Dar una respuesta completa
- Hallar el mismo resultado de otra manera.
- Verificar por apreciación que la respuesta es adecuada.
Documento elaborado por Eduteka con base en experiencias de cualificación docente llevadas a cabo por la Fundación Gabriel Piedrahita Uribe en las Instituciones Educativas: a) INSA (Cali); b) Antonio Lizarazo (Palmira); Harold Eder (Palmira); y, Semilla de la Esperanza (Palmira).
Este contenido ha sido publicado originalmente por EDUTEKA en la siguiente dirección: eduteka.icesi.edu.com



























Los documentos publicados, para el trabajo pedagógico son muy interesantes. Agredecidos por compartir.