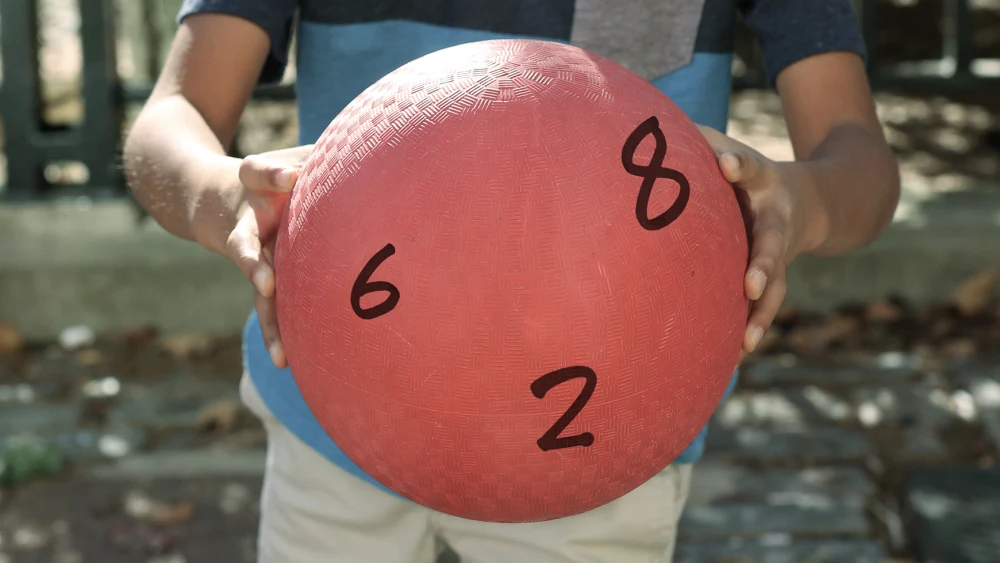No todos pensamos igual y por lo tanto no todos aprendemos igual. Tradicionalmente se empleaban métodos de enseñanza-aprendizaje basados en un único modelo de pensamiento. De este modo los alumnos y alumnas que no se adaptaban al modelo acababan condenados al fracaso tras dar varias vueltas por el sistema.
Recientemente la teoría de las inteligencias múltiples de Howard Gardner y teorías sobre los estilos de aprendizaje, ponen de manifiesto las diferentes maneras de ser inteligente y por lo tanto las diferentes formas de aprender. Atender a las diferencias de cada uno y ofrecer así una enseñanza repleta de experiencias de aprendizaje no es una tarea sencilla, suele suponer importantes quebraderos de cabeza para los educadores. La enseñanza multisensorial es una metodología que aparece como alternativa que hace posible atender a las diferentes inteligencias y estilos de aprendizaje.
Compartimos con fines educativos – pastorales la publicación del portal Understood: 8 técnicas multisensoriales para enseñar matemáticas escrito por Brendan R. Hodnett.
8 técnicas multisensoriales para enseñar matemáticas
La enseñanza multisensorial no sirve solo para la lectura. También puede ayudar a los chicos que tienen dificultades con las matemáticas, como es el caso de la discalculia. El uso de la vista, el tacto, la audición y el movimiento puede facilitar entender lo que representan los números y los símbolos. Estas son ocho técnicas multisensoriales para enseñar matemáticas.
1. Visualizar con cuentas o cereal
Usar cuentas, granos o cereal como objetos manipulativos es una manera excelente para que los chicos representen operaciones matemáticas. Por ejemplo, los chicos podrían obtener el resultado total añadiendo más cuentas. O podrían averiguar cuánto queda quitando algunas. También puede agrupar diferentes cantidades de objetos para multiplicar o dividir.
Al agregar y quitar esos objetos y ver cómo cambian las cantidades, los niños entienden de una manera concreta cómo funcionan esas operaciones matemáticas. Los objetos manipulativos también pueden ayudar a que los chicos desarrollen el sentido numérico y entiendan las cantidades.
2. Construir con cubos y fichas de colores
Al usar estos objetos para construir figuras, permite que los niños prueben fórmulas para medir cosas. Les da una idea concreta de las propiedades a través de las figuras que crean. Usar fichas o cubos también es excelente cuando se enseñan patrones numéricos y operaciones.
Por ejemplo, una maestra puede apilar objetos en grupos de 2, 4, 6 y 8, y después pedir a los estudiantes que completen los siguientes tres grupos siguiendo el mismo patrón (añadiendo dos cada vez). Así la maestra ayuda a los estudiantes a que relacionen los objetos con los números que los representan.
3. Dibujar problemas matemáticos
Dibujar problemas matemáticos es el siguiente paso después de trabajar con materiales manipulativos como cuentas o fichas de colores. Es una manera en que los chicos muestran cómo piensan y los conduce a poder escribir oraciones numéricas con números y símbolos.
Por ejemplo, un maestro podría pedir a los estudiantes que resuelvan la multiplicación: 4 x 6 dibujando 6 grupos de 4 manzanas. O el niño podría colorear 4 filas de 6 cuadrados en un papel cuadriculado. Cuando hayan terminado verán 4 grupos de 6 o 24 cuadrados coloreados.
4. Percutir los números
El acto de percutir los números puede ayudar a los chicos a relacionar símbolos con las cantidades correspondientes y “sentir” el valor. Esto es especialmente útil cuando se trabaja con múltiplos.
Por ejemplo, la maestra podría pedir a los alumnos que enumeren los múltiplos de 4. El niño empezará a golpetear grupos de 4 al mismo tiempo que los cuenta. El cuarto número se percute más fuerte y se anota (1, 2, 3, ¡4! 5, 6 , 7, ¡8! 9, 10, 11 ¡12!). Al final, el niño tendrá una lista que puede usar para resolver problemas de multiplicación y división.
8. Hacer conexiones musicales
Existen muchas maneras de conectar las matemáticas con la música. Por ejemplo, los niños pueden utilizar canciones para memorizar algoritmos o reglas matemáticas. Y tocar notas musicales puede ayudar a que los niños aprendan fracciones y a agrupar.
Por ejemplo, una maestra podría tocar una nota en un teclado y mantenerla por cierto tiempo. Esto es la “nota completa”. Después los estudiantes la repetirán. A continuación, la maestra podría preguntar, “¿cuántos cuartos de nota hacen una nota completa?”. Después de discutirlo, la maestra o un alumno podría tocar cuatro notas cortas que en total duren lo mismo que la nota completa.

6. Incluir movimiento en las matemáticas
Usar movimiento al practicar y enseñar matemáticas es una manera entretenida de ayudar a los estudiantes a retener lo que han aprendido. Existen muchas maneras de hacerlo. Por ejemplo, los niños pueden demostrar ángulos rotando su cuerpo mientras usan un aro de hula hula.
Este es un ejemplo típico en el salón de clases. Un maestro escribe números en una pelota grande (podrían ser números enteros, fracciones o decimales). Los estudiantes se la van pasando y, cuando un alumno la atrapa, tiene que hacer una operación matemática con los dos números escritos debajo de donde sus manos hayan agarrado la pelota.
7. Construir con bloques de base diez
Estos bloques vienen en diferentes tamaños representando 1000 (un “cubo”), 100 (un “plano”), 10 (un “largo”) y 1 (una “unidad”). Los chicos pueden formar números con ellos para identificar el valor de la posición (también pueden usarlos para resolver operaciones, mostrar reagrupamiento y encontrar patrones).
Por ejemplo, un maestro puede pedir a un estudiante que “construya” el número 145 usando los bloques. El estudiante tendrá que seleccionar un bloque de 100, 4 bloques de 10 y 5 bloques de 1. Después, el maestro podría preguntar, “¿qué dígito tiene el valor más grande: 1, 4 o 5?”.

8. Crear una tabla de una centena
Una tabla de una centena puede ayudar a los chicos con dificultades matemáticas a ver las relaciones entre números. Por ejemplo, un estudiante podría tener una cuadrícula de 100 (un cuadrado grande dividido en 100 cuadrados más pequeños). Se le podría pedir que sombree ¼ de toda la cuadrícula. Después tendrá que averiguar el número de cuadrados coloreados (25). La conexión es que ¼ significa lo mismo que 25 de 100, o que el 25 por ciento.

Este contenido ha sido publicado originalmente por Understood en la siguiente dirección: understood.org /Autor: Brendan R. Hodnett.
Recomendamos a la Comunidad Educativa Digital tener en cuenta que, el enlace y/o la carpeta en donde están alojados los libros, recursos y/o materiales, no es administrado por la Web del Maestro CMF, pueda ser que en cuestión de días (o según el tiempo transcurrido desde su publicación), los enlaces no funcionen y el material ya no se encuentre disponible. Gracias por su comprensión.
ENLACE DE LECTURA:
¡Comparte y así más docentes utilizarán estos recursos gratis! Muchas gracias.
MÉTODO MULTISENSORIAL PARA EL APRESTAMIENTO A LA LECTO ESCRITURA